Genetics Problem and Combinations

In the Saskatchewan Grade 9 textbook, there is a lab on genetics (page 57).  One of the questions is to figure out how many different combinations of fruit fly possibilities based on the following traits

• Long Legs (L) or Short Legs (l)
• Tan Colour (C) or Ebony Colour (c)
• Long Wings (W) or Stubby Wings (w)

 Note that capitals denote dominant alleles and lower case denote recessive alleles.  I looked up the definition of combinations and then relalised that this involved selecting 1 item from each of the three sets which are possible for each of the three traits:

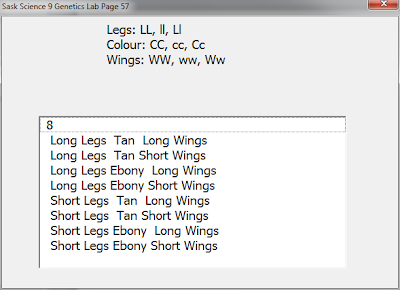
• {LL, ll, Ll}
• {CC, cc, Cc}
• {WW, ww, Ww}

 Note that

• LL and Ll are both long legs, whereas ll is short legs
• CC and Cc are both tan colour, whereas cc is ebony colour
• WW and Ww are both long wings, whereas ww is short wings

So, I would think the sets could be reduced to

• {LL, ll}
• {CC, cc}
• {WW, ww}

Now, I got rather tired of trying to figure out from the math definitions what the possible unique combinations of the three sets were, so I wrote a brute force computer program in VBA (code here) and found that it was 8.  So, of the 27 possibilities of genotypes (used a triple loop over the three traits), there are 8 unique phenotypes. I think since homozygous dominant and heterozygous dominant result in the same trait, it must be be 2^3?  Note, if we just loop over the reduced sets, it's three loops over 2 items:

LL CC WW = Long legs, Tan, Long Wings
LL CC ww = Long legs, Tan, Short Wings
LL cc WW = Long legs, Ebony, Long Wings
LL cc ww = Long legs, Ebony, Short Wings
ll CC WW = short legs, Tan, Long Wings
ll CC ww = short legs, Tan, Short Wings
ll cc WW = short legs, Ebony, Long Wings
ll cc ww = short legs, Ebony, Short Wings

I think it would have been even easier to write the code in Python, but I wouldn't have the GUI interface easily like I do with VBA.