In computer science, I often refer to two infinite alternating series:
ln(2):
and the Leibniz expansion of π/4:
When I saw these two infinite series in first year calculus, I was fascinated that such a simple pattern would result in something meaningful (it made me think there must be a God indeed!).
Now, π is a familiar irrational number, but e (Euler's number) is less well know. When I took MAT319, Introduction to Complex Analysis (the only optional math class I ever took as an undergrad), we were shown de Moivre's formula
and we were shown the much simpler Euler formula:
This is the formula Richard Feynman called "one of the most remarkable, almost astounding, formulas in all of mathematics." Why is this so important? Well, the Fourier transform requires this remarkable fact!
It is much easier to deal with exponentials than trig functions, so Fourier transforms are usually expressed as above. Why are Fourier transforms so important? Well, any application of digital signal processing requires it! When we try to remove noise from a signal (TV, radio, seismic etc), we need to be able to find the frequencies in the signal and the Fourier transform does that for us. So the images we see from various earth orbiting satellites like RadarSAT would not be possible without the Fourier transform (and Euler's formula). Euler's number (e) is a remarkable number indeed!
This example of using Audacity to analyse sound uses the Fourier transform. The frequency spectrum was computed with a Fast Fourier Transfer (FFT).
Now, I am not very good at mathematics, but I do admire and appreciate it's beauty and utility. That's probably why I admire Michael Faraday above all other scientists (he wasn't very good at math like James Clerk Maxwell was). When some of my computer science students said "your smart", I rebutted, "no I'm not" and told the story of my ordeal in APM346 (Partial Differential Equations). The class was taught by G F D Duff, FRSC. I was confused from the very start because he used a different notation from the textbook he assigned (and I'm just not that great at math). When he walked in to return the midterms, he said "the grades ranged from 0 to 100%. The class average was 33%" and then proceeded to get on with the class. The guy sitting next to me said "Hey, I did twice as well as you - I got 2/20". Seeing failure in my future, I went to see a physics prof and asked if I could take the geophysics classes next year if I failed the class. He told me "stay in the class, if he doesn't change the grade, governing council will". So, I stayed in the class, didn't bother to study for the 60% final (because I had quantum mechanics the day before and was in low spirits), answered only 2 of the 6 question on the final exam (I was admiring the woodwork in West Hall, University College for the last 15 minutes contemplating my failure). I got 52% (D-) and was so happy to pass!
It's not being 'smart' that matters. It's the willingness to learn something new. And, as I get older, I realise that if something is difficult, it means I'm actually learning something new. One of the concepts from APM346 that confused me was Bessel Functions. During coffee break in grad school, one of my colleagues moved his styrofoam cup across the table and said, "look at the Bessel functions" in response to the ripples that were forming in the cup. It was at that time it dawned upon me that Bessel functions are used to solve boundary value problems in cylindrical coordinates. You don't have to know why they work (at least as a scientist), you just have to know that for cylindrical geometry, Bessel functions work! And, for spherical coordinates, Legendre polynomials work (I heard that in Derek York's Physics of the Earth class in fourth year).

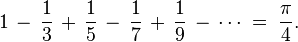


No comments:
Post a Comment